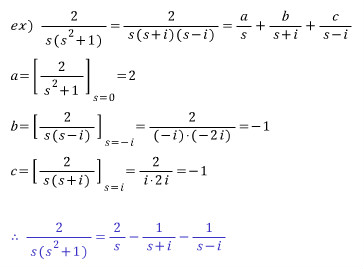(1) 분모가 일차식으로만 인수분해될 때
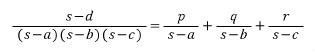
로 부분분수 전개를 할 때 각 항의 분자 p , q , r 을 구해봅시다.

같은 방법으로

이제 분모에 일차식의 거듭제곱이 있을 경우를 생각해봅시다.





일반적으로 아래와 같습니다.

(예제)


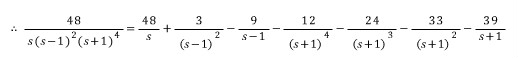
(2) 분모가 2차 이상의 식으로 인수분해될 때
이 때는 미정계수법을 이용하여 문제를 해결합니다.

위와 같이 부분분수 전개될 때 a, b, c 를 구해봅시다.
참고로 부분분수 전개될 때 분모가 n차식이면 분자는 (n-1)차식으로 두어여 합니다.
위 문제의 경우 s-1 의 분자는 상수항, s²+2s+4 의 분자는 일차식으로 두어야 합니다.
우변을 통분하면
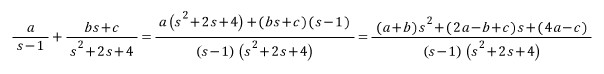
따라서
 이 되며
이 되며
분자를 비교하면
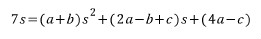
위 식은 s 의 값에 관계없이 항상 성립해야 하는 s 에 대한 항등식이므로 양변의 계수가 서로 같아야 합니다.
a+b = 0 , 2a-b+c = 7 , 4a-c = 0
연립하여 풀면
a=1 , b=-1 , c=4

※ 두번째 방법은 분모가 일차식의 곱으로만 인수분해되는 식에서도 사용할 수 있으며
더 이상 인수분해가 되지 않는 이차식을 복수소을 포함하는 일차식으로 인수분해하여 첫번째 방법으로
해결할 수도 있습니다.