그런데, 각을 표현하는 다른 방법으로 라디안(radian)이 있습니다. 보통 라디안은 부채꼴의 중심각을 가지고 설명되는데, 아래 그림과 같이 호의 길이가 반지름과 같게 되는 만큼의 각을 1 라디안(radian)이라고 정의합니다.

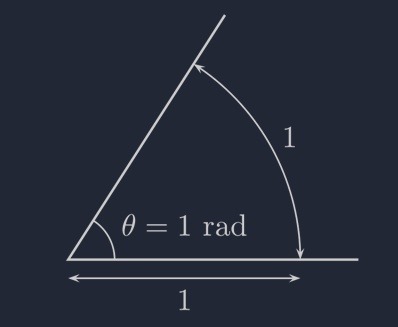
정의에 따르면 왠지 라디안은 반지름에 대한 상대적인 각도의 단위처럼 생각됩니다. 하지만 radian은 degree처럼 절대적인 각도의 단위입니다. 실제로 1 radian은 약 57.3도에 해당하는 각입니다. 그러면 2 radian은 약 114.6도가 되겠지요. 여기서 우리는 degree보다는 radian이 훨씬 큰 각의 단위라는 걸 알 수 있습니다.

반지름이 3이고 중심각이 2 radian인 부채꼴이 있습니다. 그러면 이 부채꼴의 호의 길이는 얼마일까요? radian의 정의에 의해 답은 6입니다. 반지름과 중심각의 크기만 알면 호의 길이를 이렇게 쉽게 구할 수 있다는게 신기하지 않나요? 반대로, 호의 길이가 6이고 반지름이 3인 부채꼴이 있다면 이 부채꼴의 중심각은 얼마일까요? 바로 2 radian입니다. 즉, 약 114.6도입니다. 부채꼴 도형에서 반지름, 중심각, 호의 길이 3가지 중에 2가지만 알면 다른 한가지는 곧바로 구할 수 있게 됩니다.

자동차가 달리고 있는데 오른쪽으로 10도 틀으라고 하면 대략 얼마나 돌려야 할지 감이 올 것입니다. 그런데, 만일 오른쪽으로 0.5 radian 돌려라고 한다면 도대체 이게 어느 정도의 각인지 도무지 감이 오지 않을 것입니다. 이와 같이 우리에게 친숙한 각의 단위는 degree입니다.

그러면, 우리에게 친숙한 degree로만 각을 표현하면 좋을텐데 왜 이렇게 복잡하게 radian이라는 것을 도입해서 문제를 어렵게 하는 걸까요? 사실 저도 이유는 잘 모릅니다. 하지만 분명한 것은 우리 사람이 선호하는 각 체계는 degree인 반면 컴퓨터나 수학에서 주로 사용되는 각 체계는 radian이라는 것입니다. 그래서 표준을 정하거나 공동작업을 할 때 종종 각을 어떻게 표현할 것인가를 두고 사람들끼리 논쟁이 일어나기도 합니다. 사람을 중심에 놓고 생각하는 사람들은 degree를 사용하자고 주장하고, 다른 한편에서는 어차피 컴퓨터에서는 radian으로 고쳐서 사용해야 하기 때문에 계산의 효율성을 위해서 radian을 사용하자고 주장합니다. 

컴퓨터에서 프로그램을 개발할 때에도 degree와 radian을 변환하는 일이 수시로 발생합니다. 사용자에게 각을 입력받을 때는 보통 degree로 입력받은 후 이를 내부적으로 radian으로 고쳐서 필요한 계산을 수행합니다. 그리고 계산된 결과를 보여줄 때는 다시 사람에게 친숙한 degree로 변환하여 보여줍니다. 이러한 변환작업은 사실 번거롭긴 하지만 어쩔 수 없는 일이기도 합니다. 

그렇다면 degree와 radian은 어떤 변환 관계를 가지고 있을까요? 180도는 π radian입니다. 여기서 π(파이)는 3.1415926535... 의 값을 갖는 무한소수로 원주율을 말합니다(원주율 π는 원의 둘레가 지름의 몇 배나 되는지를 그 동안 수학자들이 열심히 노력해서 찾은 값인데, 원둘레 = 3.1415926535..×지름 = π×2r 이 됨을 찾아냈고 이 상수를 원주율 π라 명명한 것입니다). 이 관계식을 이용하면 다음과 같이 자유롭게 degree와 radian의 단위를 변경할 수 있습니다.

180 degree = π radian

1 degree = π / 180 radian

x degree = x * π / 180 radian

π radian = 180 degree

1 radian = 180 / π degree

x radian = x * 180 / π degree

좀전에 자동차 예에서 나온 0.5 radian을 위 수식을 이용하여 degree로 고치면 0.5 * 180 / 3.1415926535 = 28.64788... degree 정도가 됩니다. 그러나, 수식을 이용하지 않고도 대략적인 radian의 값을 파악하는 방법이 있습니다. 그건 먼저 머리속에서 부채꼴을 하나 상상합니다. 그 부채꼴의 호의 길이는 반지름과 같은 길이를 갖도록 합니다. 그러면 그 부채꼴의 중심각이 1 radian입니다. 이제 0.5 radian을 구하고 싶으면 상상속의 그 부채꼴의 중심각을 2등분하면 됩니다. 그러면 대략적으로 0.5 radian이 어느정도의 각인지 알 수 있을 것입니다.